Alipäästösuodatin

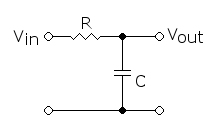
Alipäästösuodatin eli alipäästösuodin (eng. low-pass filter) on suodatinrakenne, joka päästää läpi matalataajuiset ja vaimentaa eli suodattaa korkeataajuiset signaalit.^[1]

Alipäästösuodatinta on loivalla vaimennuksella yleisesti käytetty radiovastaanotinlaitteissa äänenvärinsäätimissä (Tone-säädin) ja audiopäätevahvistimissa erillisessä korkeiden äänten Treble-säätimissä. Niiden kytkentä perustuu yleisesti analogisen yksinapaisen RC-suodattimen kytkentään.

Suodatin voi olla komponenteilla toteutettu analoginen suodatin tai tietokoneella signaalia käsittelevä digitaalisuodatin.

Yksinkertainen analoginen RC-alipäästösuodatin voidaan toteuttaa vastuksen ja kondensaattorin jännitteenjakokytkennän avulla (kuvassa). Matalilla taajuuksilla kondensaattorin läpi kulkee vähän virtaa, jolloin vastuksen yli muodostuu vain pieni jännitehäviö ja signaali ei juurikaan vaimene. Korkeilla taajuuksilla kondensaattori näyttää lähes oikosululta, jolloin ulostulojännite on lähellä nollaa. Kuvan RC-piirin lähtö- ja tulojännitteen välillä vallitsee riippuvuus

${\displaystyle {\Big |}{\frac {V_{\mathrm {out} }}{V_{\mathrm {in} }}}{\Big |}={\frac {1}{\sqrt {1+(2\pi RCf)^{2}}}}}$.

Taajuus ${\displaystyle f_{0}={\frac {1}{2\pi RC}}}$ on alipäästösuodattimen ominaistaajuus.

Ensimmäisen asteen alipäästösuodattimen yleinen siirtofunktio on muotoa

${\displaystyle {\frac {U_{\mathrm {out} }}{U_{\mathrm {in} }}}=H(s)={\frac {1}{s+1}}}$

ja toisen asteen siirtofunktio on muotoa

${\displaystyle H(s)={\frac {1}{s^{2}+2Ds+1}}}$,

missä ${\displaystyle s}$ on Laplace-muuttuja ja ${\displaystyle D}$ suodattimen vaimennusvakio. Siirtofunktio voidaan myös kertoa vakiotermillä, mikäli suodatin sisältää vahvistusta tai vaimennusta. Tekemällä sijoitus ${\displaystyle s=j\omega }$ saadaan lauseke, joka kertoo suodattimen siirtofunktion sinimuotoisille jännitteille kompleksilukuna. Kompleksiluvun itseisarvo kertoo lähtö- ja tulojännitteen amplitudien suhteen ja kompleksiluvun kulma kertoo signaalien välisen vaihesiirron. Sijoittamalla ${\displaystyle \omega =0}$ nähdään, että molempien siirtofunktioiden arvo on tasajännitteellä 1, toisin sanoen signaali pääsee vaimentumatta suodattimen läpi. Koska muuttuja ${\displaystyle s}$ on nimittäjässä, taajuuden kasvaessa lähtöjännite pienenee.

Useampiasteinen alipäästösuodatin saadaan rakennettua ensimmäisen ja toisen asteen siirtofunktioiden tulona. Käytännön kytkennöissä tämä voidaan toteuttaa kytkemällä peräkkäin erilaisia suodatinlohkoja.

Vaimennusvakion ${\displaystyle D}$ sijasta alan kirjallisuudessa käytetään myös hyvyyslukua Q ja vaimennuskerrointa ${\displaystyle d}$. Näiden välillä vallitsee yhteys

${\displaystyle Q={\frac {1}{2D}}={\frac {1}{d}}}$

• Elektroniikan suodattimet

• Wanhammar, Lars: Analog Filters Using MATLAB. Springer International Publishing, 2009. ISBN 978-0-387-92766-4 Teoksen verkkoversio Viitattu 2.7.2020.